728x90
반응형
목적
- 하노이의 탑 알고리즘을 가시화하여 이해를 쉽게함
- 가시화된 알고리즘을 재귀 함수로 구현함
- 구현할 함수는 아래 2개임 ( A탑에 위치한 원반 개수는 N)
- int count_hanoi(int n) : A에서 C까지 N개의 원판을 이동시키는데 필요한 전체 개수
- void hanoi(int n, int from, int to) : n번째 원판을 From에서 To로 이동시킴

탑 이동 알고리즘 (Hanoi Function)
- 하노이 탑의 이동을 재귀로 구현할 땐 아래 이미지의 이동 방식을 알면 됨

- N이 2보다 더 큰 경우도 가장 밑에 있는 N번째 원판과 그위의 나머지 원판으로 부분을 나누면,
위와 같은 방식으로 이동이 가능함
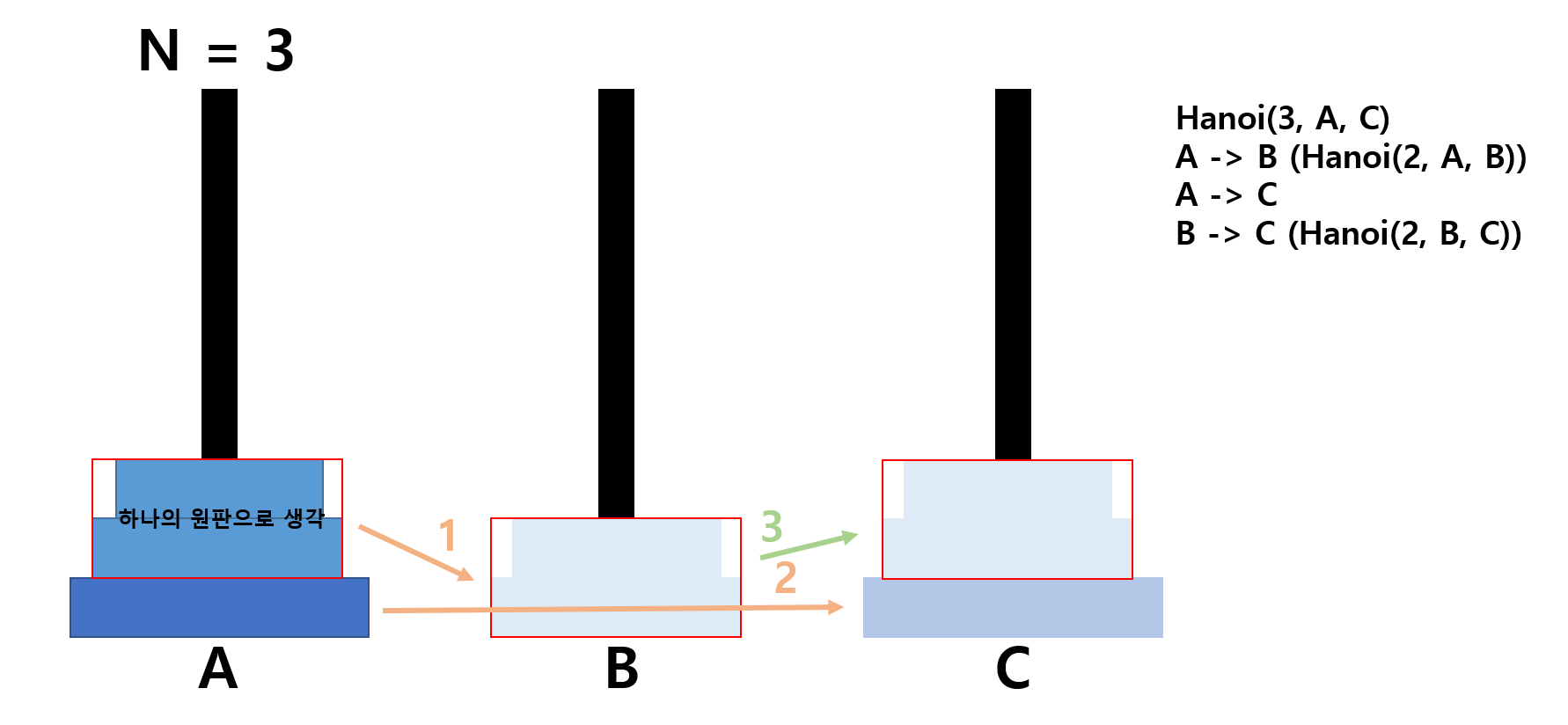
- hanoi(2, A, B)와 hanoi(2, B, C)의 이동을 직접 나열해보면 아래와 같다

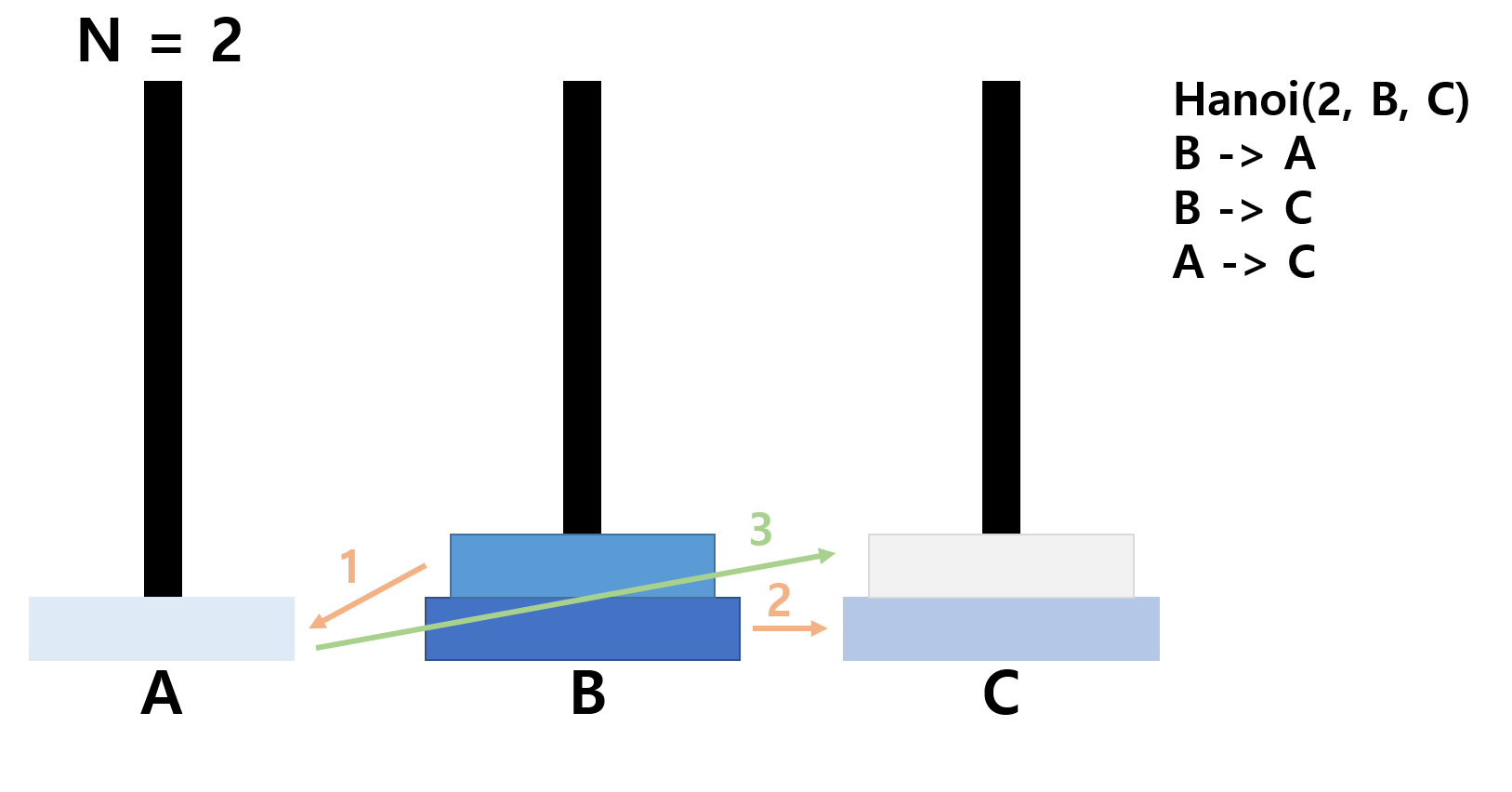
- hanoi(n, from, to) 함수는 아래와 같은 규칙을 갖는다.

원판의 개수로 전체 이동 횟수 구하기 (Count_Hanoi Function)
- 하노이 탑의 이동 횟수는 아래와 같은 형태의 수열을 이루고 있다.

- 원판의 개수가 N일 때, 원판을 이동 시키는 횟수는 '2의 N제곱 -1' (2^n -1)
- 제곱연산은 1 << N으로도 표현이 가능함 (비트연산)
Ex) 0001 << 3 -> 1000(2), 8(10)
원판 개수 = 1 << N -1
소스 코드
- 아래 코드에선 탑을 1~3으로 표현함.
#include<iostream>
using namespace std;
void count_hanoi(int n){
cout << (1 << n) -1 << "\n";
}
void hanoi(int n, int from, int to) {
if (n == 1){
cout << from << " " << to << "\n";
}else{
hanoi(n - 1, from, 6 - from - to);
cout << from << " " << to << "\n";
hanoi(n - 1, 6 - from - to, to);
}
}
int main() {
int n;
cin >> n;
count_hanoi(n);
hanoi(n, 1, 3);
return 0;
}
결과

728x90
반응형
'코딩테스트 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 순열과 조합 (0) | 2022.04.21 |
|---|---|
| [알고리즘] 다익스트라(Dijkstra) (0) | 2022.04.11 |
| [자료구조] 우선순위 큐 - 작성 중 (0) | 2022.04.11 |
| [알고리즘] DFS/ BFS (0) | 2022.02.05 |
| [알고리즘] 달팽이 배열 채우기 (0) | 2021.11.06 |
| [알고리즘] 함수 (0) | 2021.10.11 |